Many of the top large language models today such as GPT-4, Claude 3 and Gemini are closed source, so a lot about the inner workings of these models is not known to the public. One justification for this is usually the competitive landscape, since companies are investing a lot of money and effort to create these models, and another justification is security, since it is easier to attack models when more information is available. In this post we study a recent research paper with authors from Google DeepMind, titled: “Stealing Part of a Production Language Model”, which presents a model-stealing attack that extracts internal information from black-box language models, and the attack is performed via a standard API access where the attacker is using the API to get internal data about the model behind the API. Specifically, the internal data being stolen is the embedding projection layer, the last layer of the model, and the researchers estimate that it would cost under 2000$ in queries to retrieve the embedding projection layer of gpt-3.5-turbo.

Before diving in, if you prefer a video format then check out the following video:
The Attack Targets
Before diving into the attack details, let’s first learn more about when the attack is possible. So, who is the target for the attack presented in the paper? The answer is production language models that are accessible via APIs, that expose log probabilities or a logit bias.
- By log probabilities the meaning is that we do not just get a generated token, but rather a list of tokens with their log probabilities, so we can learn which are the most possible tokens and how likely each one of them to be the next one.
- By logit bias the meaning is that we can impact the probabilities of tokens we wish to control to impact the chances of them being the next token. For example, we can exclude a certain token from the output by pushing down its probability to be chosen using a significant bias.
Attack Achievements
The requirements for the attack which we’ve just mentioned include in practice multiple OpenAI models including GPT-4 and also Google’s PaLM-2. And the researchers have successfully used this attack in order to extract the entire embeddings projection layer for two Open AI language models, ada and babbage, and also to discover the hidden dimension of gpt-3.5-turbo. And as we mentioned earlier, the researchers could have extracted the entire embedding projection layer of gpt-3.5-turbo by extending the attack, with less than 2000$ in API queries. It is worth mentioning that by now OpenAI and Google already added mitigations for this attack since the attack was shared with them prior to publishing the paper.
Recover The Hidden Dimension Size
Let’s now start to dive into the attack details, starting with the most simple case of recovering the hidden dimension size only. And for start we have an assumption that the API expose full logits. Meaning that we get from the API the logits of all tokens in the model vocabulary. This is a tough requirement since in practice the APIs provide just the top log probabilities and not all of the logits, but we’ll see later that this requirement is removed.
Embedding Projection Layer Role In The Transformer
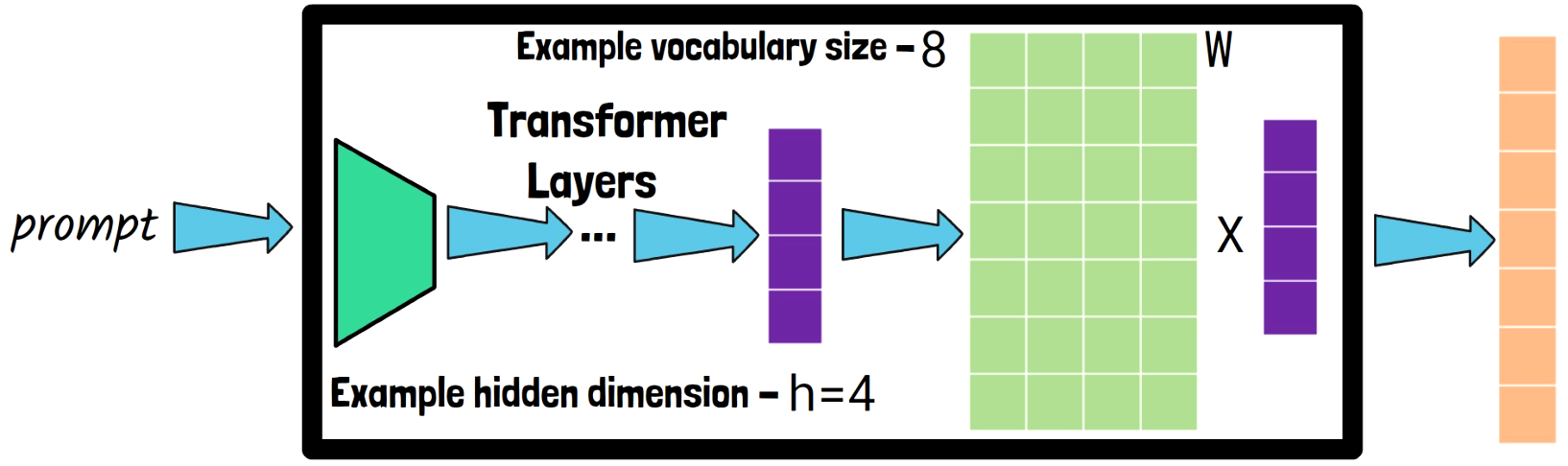
To understand how the attack is possible let’s first recall what happens in the embedding projection layer. In the above box we have a transformer model for example, and when we feed it with a prompt, the model process the prompt via all of the transformer layers, until we reach the final embedding projection layer. The input for the embedding projection layer is a vector of hidden states, in the size of the hidden dimension, where in the simple example here the size is 4. And the embedding projection layer should project this vector to the tokens in the vocabulary. We do that using a matrix multiplication, where here we simply assume we only have 8 possible tokens in the vocabulary, so the matrix is of size 8 X 4, and so after this multiplication we get a logit for each of the tokens in the vocabulary.
Key Observation For The Attack
A key observation in our example is that the matrix of the embedding projection layer has a rank of at most 4, which is the hidden dimension size, since the rank cannot be larger than the number of columns. And this is also the case since the vocabulary size is larger than the hidden dimension size, and this assumption is correct for real models as well. If a matrix has a rank of 4, then it means that each of the 8 rows of the matrix can be written as a linear combination of some 4 vectors. Ok, but how can we use that knowledge in order to discover the hidden dimension size? The answer is based on SVD which stands for singular value decomposition.
The Attack Method

We randomize n prompts, and we invoke a LLM that provides a logit vector for each of the prompts (we’ll remove this requirement later on). With the result logits, we construct a matrix Q, where each row is the logits vector for a certain input prompt. Now if we take a large enough n, we can almost be certain that it is larger than h, the hidden dimension we want to discover. However, the dimensionality is still not larger than h, since these logits vector are obtained by a matrix multiplication with the embedding projection matrix. The next step is to calculate the rank of the matrix Q which is done using SVD, which gives us the estimation for the hidden dimension size. In practice it gives us an upper bound for the hidden dimension, but the researchers mention it is very unlikely that it will be lower if we take a large enough n. And this assumption is fine as we’ll see soon with the results.
Recover The Embedding Projection Layer Weights
Let’s now move try to understand how we can not only discover the hidden dimension size, but also the actual weights of the embedding projection layer. The answer is short and here as well is based on SVD. With SVD, we can rewrite the matrix Q that we’ve built from the logits returned from the model, as a multiplication of 3 matrices 
And the researchers found out that UΣ is actually the embedding projection matrix up to a rotation.
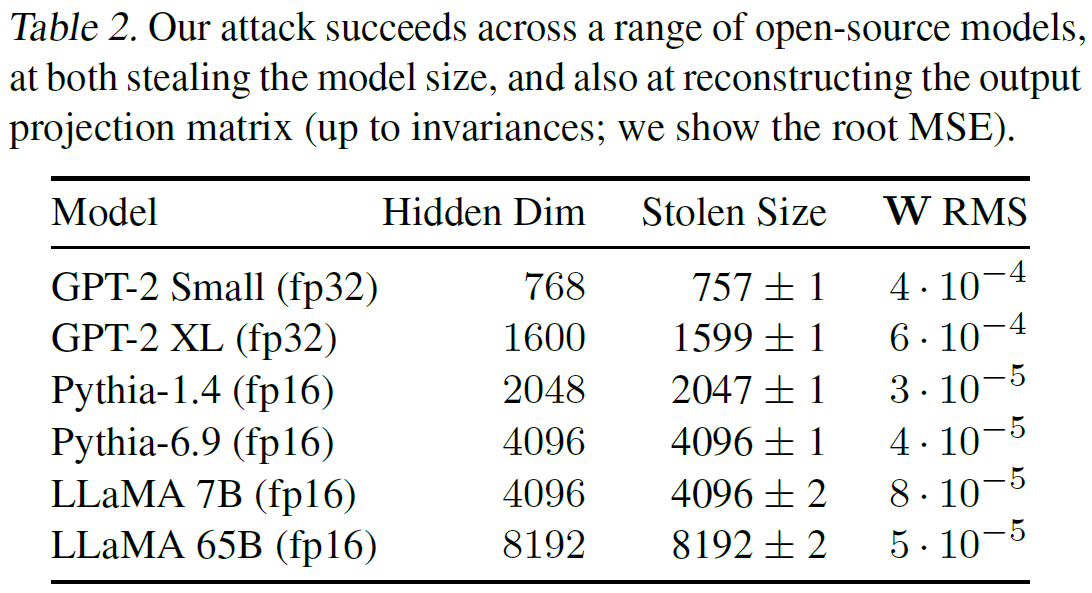
Evaluating The Attack On Open Source Models
In the following table from the paper, we can see how close the approximations are, where for the hidden dimension size, the attack extracts the correct value for the evaluated models almost precisely. And in the right column we can see the error of the extracted weights, after a search for the best rotation of the extracted matrix. For reference, this error is 100 to 500 times smaller than the error for a random guess.
Adapting The Attack To Work With Top K Log Probabilities
Until now, we’ve made a significant assumption that we can get the logit vector for each prompt, but in reality, we do not get that from the APIs. What we do get instead are the log probabilities of the most likely tokens. In order to use the attack we just saw, what we need to show is that given an API that returns the top log probabilities, we can recover the full logit vector. How can it be done?
API assumption – Returns top 5 log probabilities, and supports adding a logit bias to the API query.
Step 1 – Single API Query
First, we call the API with a large logit bias for 4 tokens only. The bias is large enough so that these 4 tokens will be part of the top 5 log probabilities. The fifth log probability in the top 5 is used as a common reference between the biased tokens. We’ll see what it means in a moment.
Step 2 – Logits From Log Probabilities
Second, we want to estimate the logit values for the 4 biased tokens. To understand how, we need a bit of math from the paper.
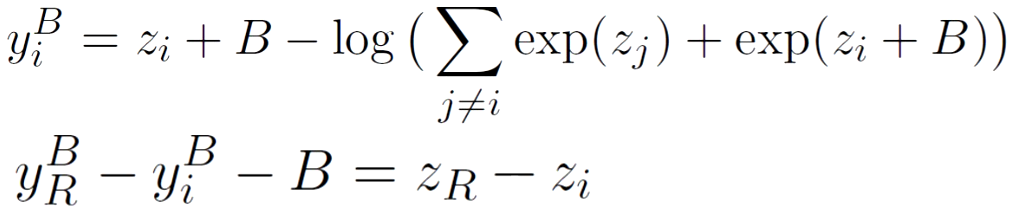
Above, we see the log probability for some biased token i. The y on the left is the log probability, and it equals to z, which is the logit, plus B which is the bias we added, and another log component that is dependent on the bias. Now if we take the log probability of the reference not biased token, marked with yR at the bottom equation, and subtract from it the log probability of a biased token and the bias B, the log component is removed and we remain with some value for the difference between the logits of the reference token and the biased token. The researchers replace the reference token logit with zero in order to get an approximation for the logits. An important observation for that approximation is that the original difference between the logits is preserved, since we use the same reference token logit value.
Step 3 – Repeat
The third step is to repeat that each time for different 4 tokens until we get the logits of all tokens.
Step 4 – Re-use Logits-based Attack
Once we have estimation for the full logit vector, we can use the same attack as we covered before when the full logit vector is available.
Attack Results On Close-Source Models
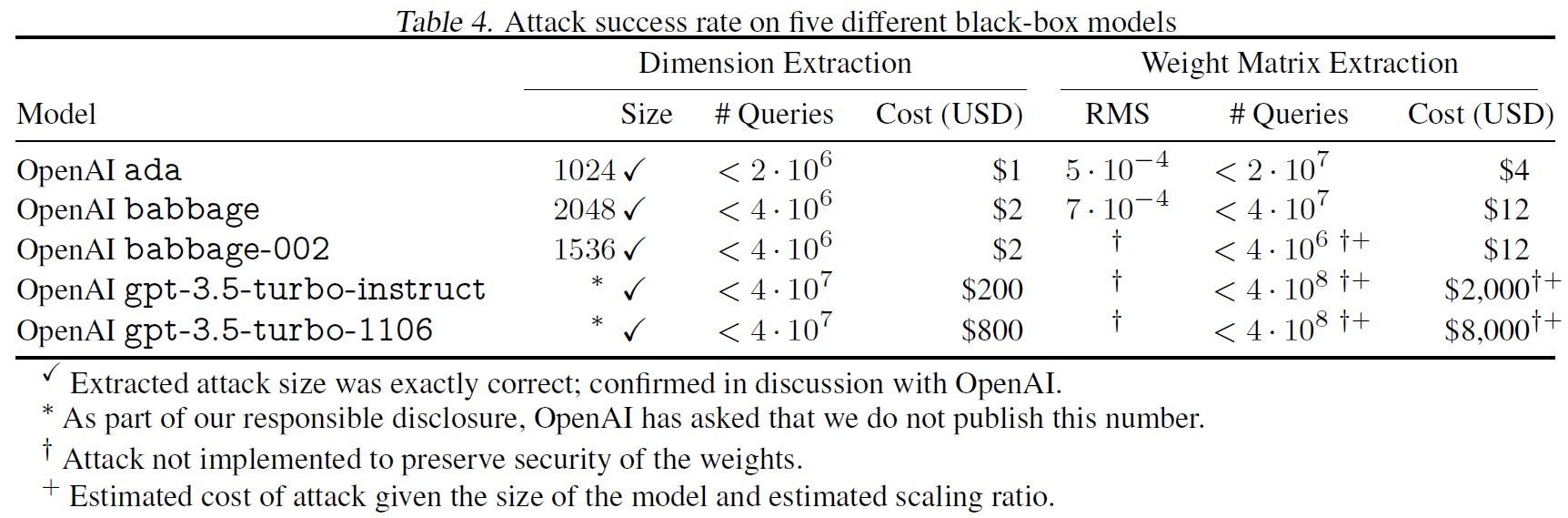
In the above table from the paper, we can see the attack results on few black box models from OpenAI. Starting with extracting only the hidden dimension, the researchers were able to obtain the precise hidden dimension of all of these models, as they have confirmed with OpenAI, but they do not disclose the numbers for gpt-3.5-turbo. They also share the cost of running the attack which is not significant. On the right we can see the error when extracting the weight matrix and the cost for doing that which is still not very significant. The attack was not executed on all of the models to preserve the security of the weights and by now defenses have been placed to against this attack.
Results With Different Attack Methods
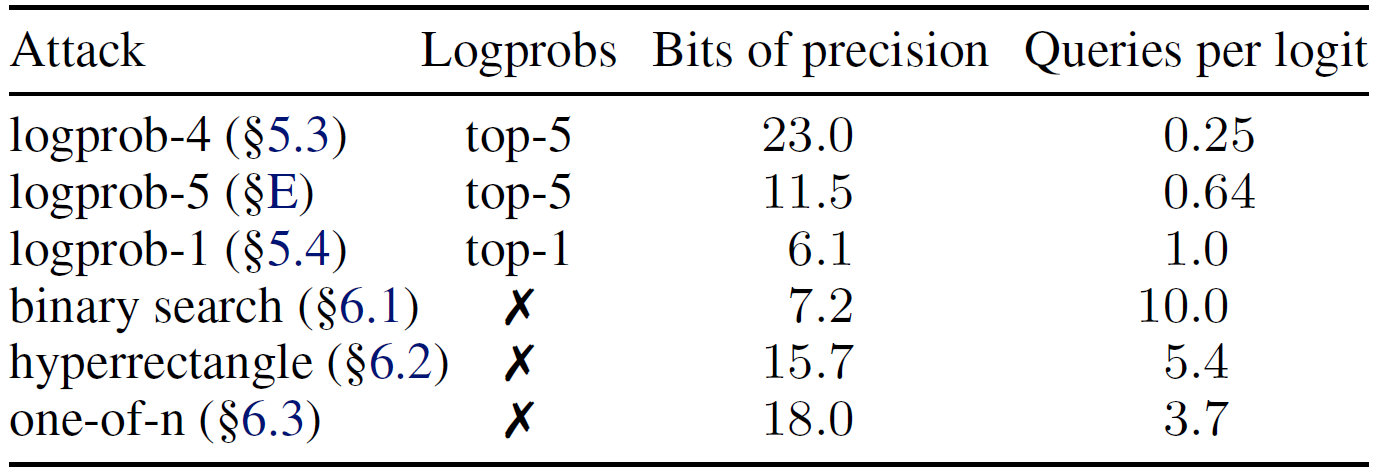
In the above table from the paper, we see comparison between different attack methods. The difference between the attack methods is how they restore the logits. We only covered the first one in this post, which achieves the best results, in the lowest cost. However, in the other methods the researchers show how the attack is possible when there is only one log prob in the API result or none at all.
References & Links
- Paper page – https://arxiv.org/abs/2403.06634
- Video – https://youtu.be/lmPdcTsy9rM
- Join our newsletter to receive concise 1 minute read summaries of the papers we review – https://aipapersacademy.com/newsletter/
All credit for the research goes to the researchers who wrote the paper we covered in this post.