In this post we dive into a recent research paper which presents a promising novel direction for fine-tuning LLMs, achieving remarkable results when considering both parameters count and performance.

Before diving in, if you prefer a video format then check out the following video:
Motivation – Finetuning a Pre-trained Transformer is Expensive
A common method to solve a problem in AI these days is to leverage an existing large pre-trained transformer model, which was already trained on huge amount of data, and in order to make it work better for the specific task that we want to solve, we usually fine-tune the model on a dedicated dataset. However, fine-tuning the entire model is expensive and not accessible for everyone. That’s why we usually use parameter-efficient finetuning (PEFT).
PEFT To The Rescue
With PEFT methods, the idea is to only update a small number of weights, to ease on the fine-tuning process. One especially known PEFT method is LoRA, where we add small adapter weights to the model layers, and only update the added weights in the fine-tuning process, while the pre-trained model weights are kept frozen.
ReFT – A Rival for LoRA?
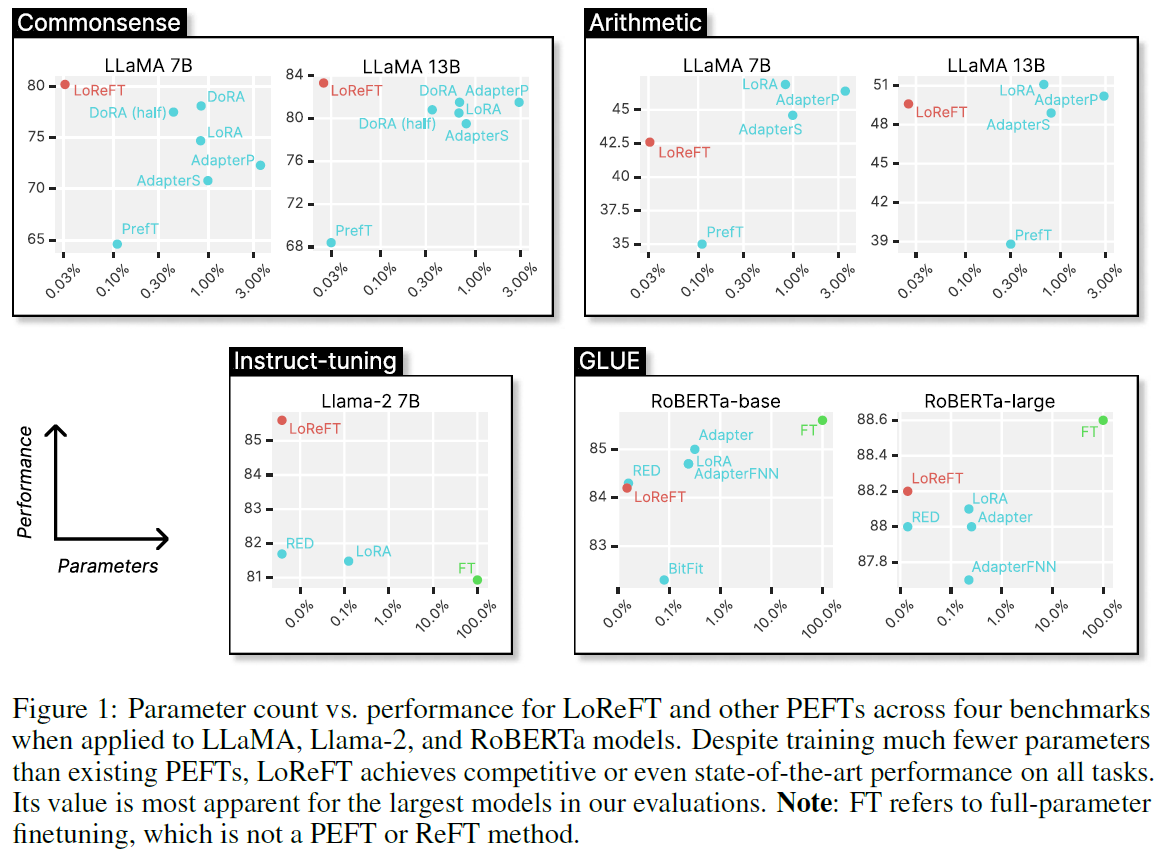
The paper we review in this post, presents representation finetuning, called ReFT, and specifically LoReFT, which requires 10-50 times less parameters than LoRA, while still providing remarkable results. We can see the potential of the new method in the following figure from the paper, where we see results for few tasks. On the y axis we see the performance on each task, and on the x axis we see the percentage of parameters that were trained. In red we see the results for the method presented in the paper, in blue we see results for multiple PEFT methods, and in green we see the results for full fine-tuning. Impressively, we see that LoReFT wins all methods in instruction following and commonsense tasks, while training a super small number of weights comparing to the model size. And on the right charts it is still competitive in performance while being the most efficient in terms of parameters count.
Explaining the idea of ReFT
Transformer Model – A Reminder
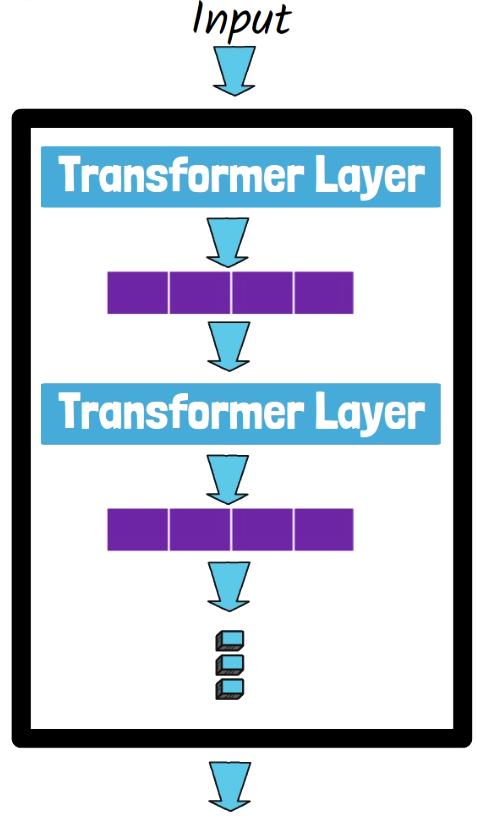
Before we move on to understand what is representation fine-tuning and how it is different than previous parameter-efficient fine-tuning methods, let’s shortly define a transformer model for example which we will later use to explain ReFT. In the image above, we have a simplified transformer model for example, where we have multiple transformer layers, each one includes a self-attention and a MLP which we treat as a black box here for simplicity. After each layer we have a vector of hidden states, which we call representations. Each representations vector is then forwarded to the following transformer layer.
LoRA Weights Are Baked Into The Transformer
With LoRA, we mentioned that we train small number of adapter weights. This is not a post about LoRA, but it is important to mention, that once trained, the weights are baked into the model. So, the representations we get in each step of the transformer are impacted by the added LoRA weights, and they are not the original representations we would get from the pre-trained transformer. This is also the case for other parameter-efficient fine-tuning methods.
Representations Grasp Rich Semantic Information
A key learning from previous research is that the hidden representations we get after each layer encode rich semantic information. By playing with the pre-trained model weights as with do with LoRA and other PEFT methods, we also impact the hidden representations that we get. This leads us to the key idea with representation fine-tuning, which is that editing the representations, as we get them from the original pre-trained model, may be a more powerful technique.
ReFT High-level Architecture
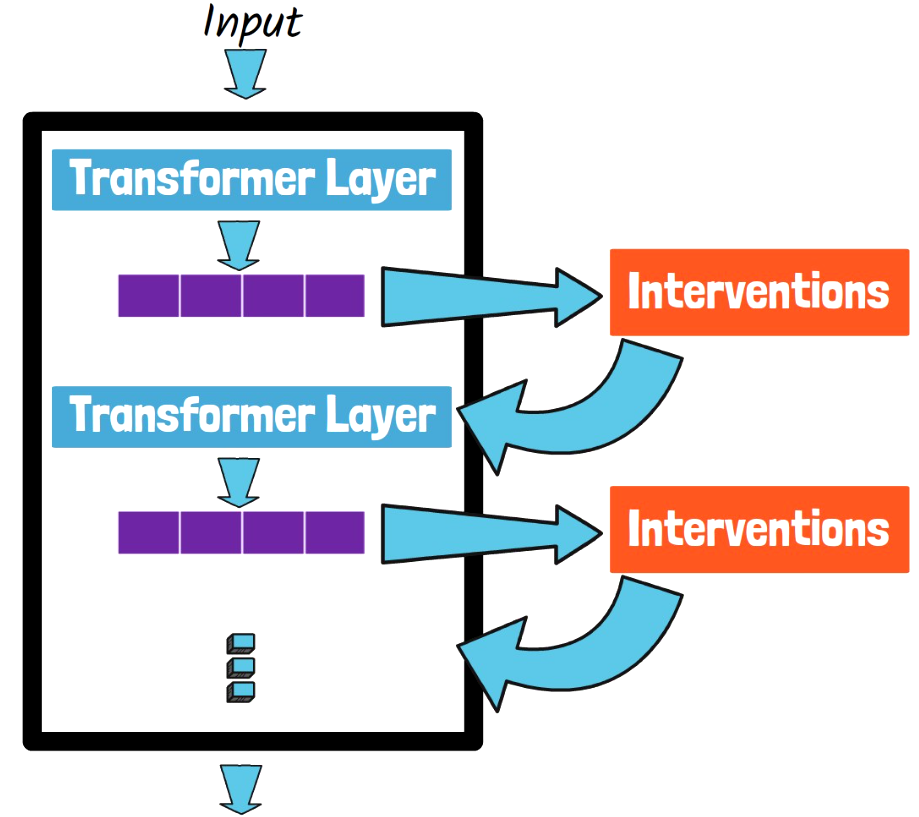
Following the above insight, with ReFT we want to edit the original representations we would get from the pre-trained transformer. The way it is being done is via interventions. What does it mean? After we get a hidden representations vector from each transformer layer, before passing them directly to the next layer, we pass the hidden representations via interventions. The interventions are small components with their own weights that we train to edit the representations to work better for specific tasks. Let’s now move on to learn more details about ReFT and understand what is the meaning of LoReFT.
ReFT Interventions In More Details
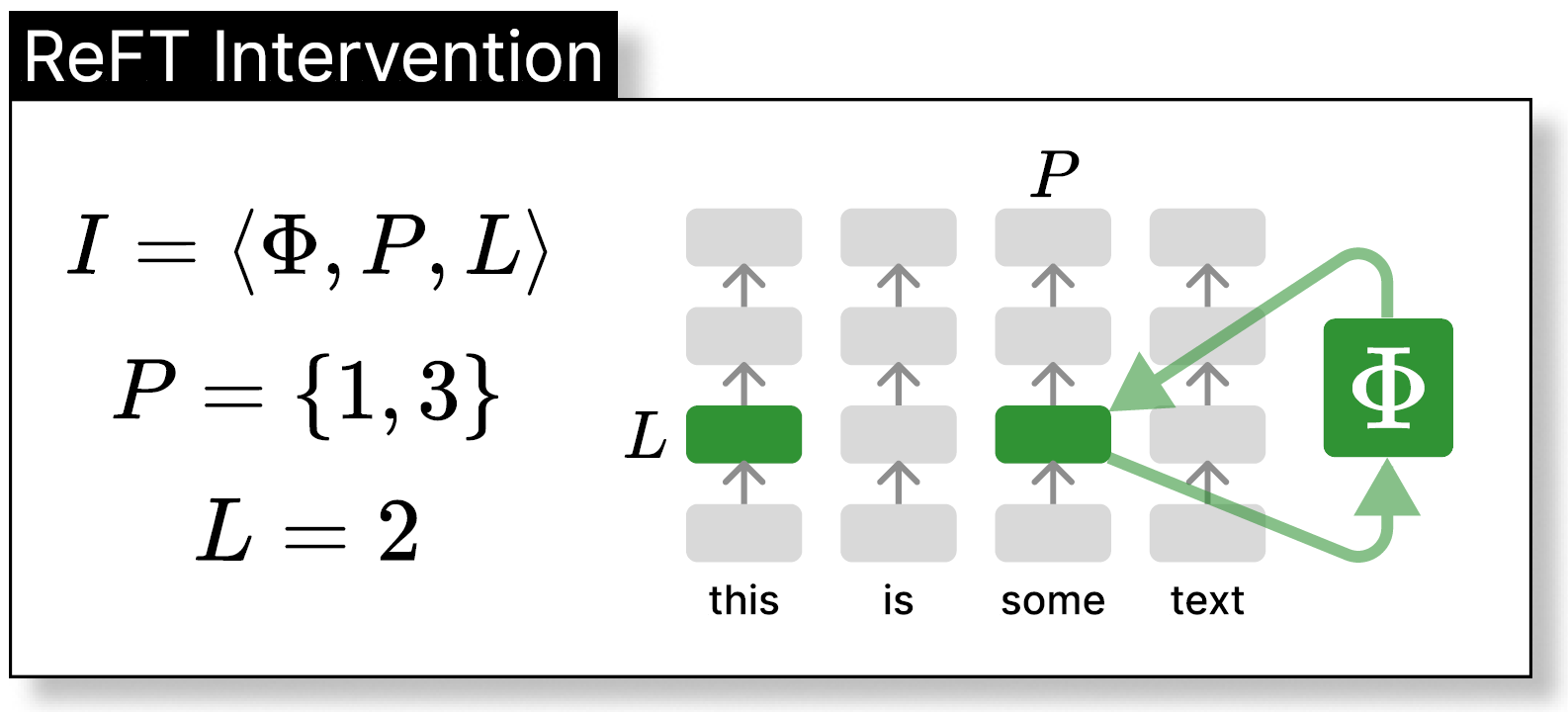
In the above figure from the paper, we can see a similar illustration to what we’ve seen a bit earlier, where we have 4 tokens at the bottom, and they are propagated up via the transformer layers, but we add more information to the intervention now. The intervention is defined by the capital letter I and it has 3 components. The first is Phi, a function to edit a representation. We see on the right that a representation for a certain token is passed via this component and then returned to the same location after the edit. The second component is P which defines which tokens are handled as part of the intervention. Meaning that the intervention will only edit the tokens defined in P, and will leave the other tokens unchanged. The last argument is L which defines the layer which this intervention is in charge of. So in the example we have here L is 2 and P includes 1 and 3 so we see the corresponding representations are colored with green.
What is LoReFT?
An important note is that ReFT is a family of methods, and we may see further research which presents novel ReFT methods in the future. In the paper we review here, the researchers introduced a specific ReFT method which is called LoReFT. LoReFT stands for Low-rank Linear Subspace ReFT, and it defines the function we use to edit the representations and the parameters that we need to train. Specifically, the function is defined with the following equation from the paper.
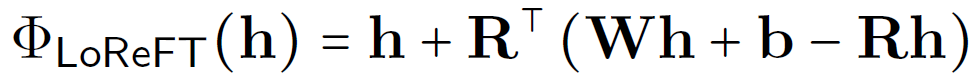
h is the representation we get from the pre-trained transformer layer, and we add to it a component which is dependent on a matrix R, a matrix W and a vector b. During training of LoReFT we train the weights of R, W and b in order to use that edit function. The code for this can be found here. The paper refers to a research about neural networks interpretability for the inspiration of this definition, which we won’t dive into in this post.
LoReFT Hyperparameters
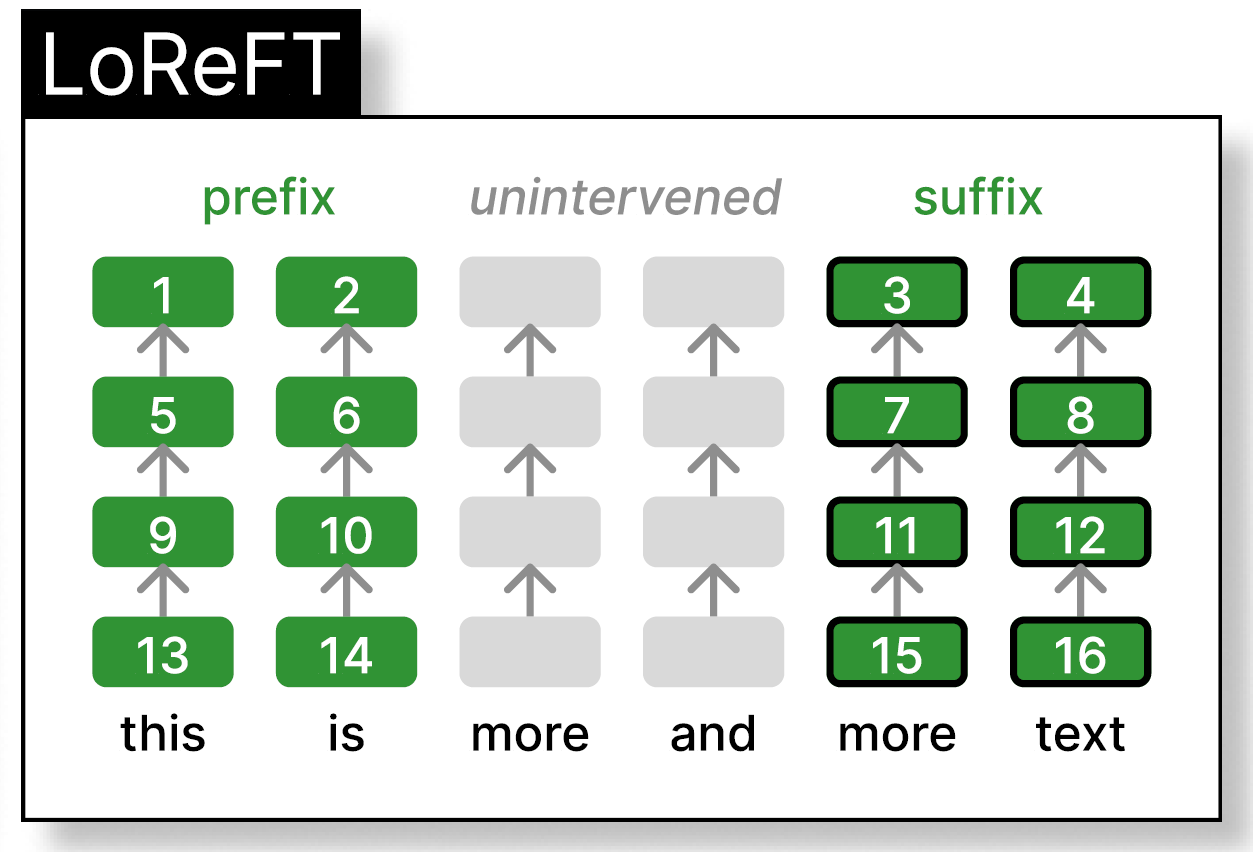
In the following figure from the paper, we can see that with LoReFT, we train interventions for prefix and suffix of the tokens, where the exact size of prefix and suffix are hyperparameters. The intervention parameters are either shared or not shared between different tokens of the same layer, and they are different between the different layers.
LoReFT Results
We saw a summary of the results in the beginning of the post and let’s now explore the results in more details.
Commonsense Reasoning
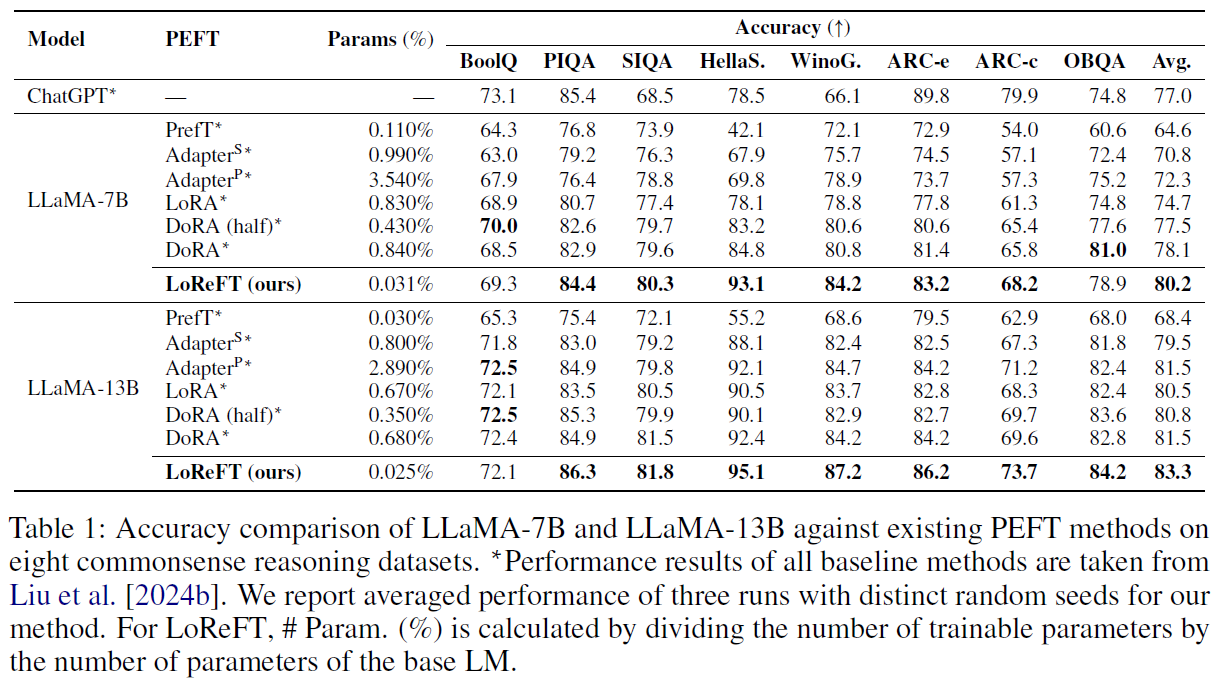
In the above table from the paper we can see the results on 8 datasets, and a comparison of different PEFT methods including LoRA and DoRA with the LoReFT method presented in the paper. First, we can notice that the params count is much lower for LoReFT comparing to the other methods. Second, even with the lower parameters count, the method beats the PEFT methods on most of the datasets and in the overall average.
Arithmetic Reasoning
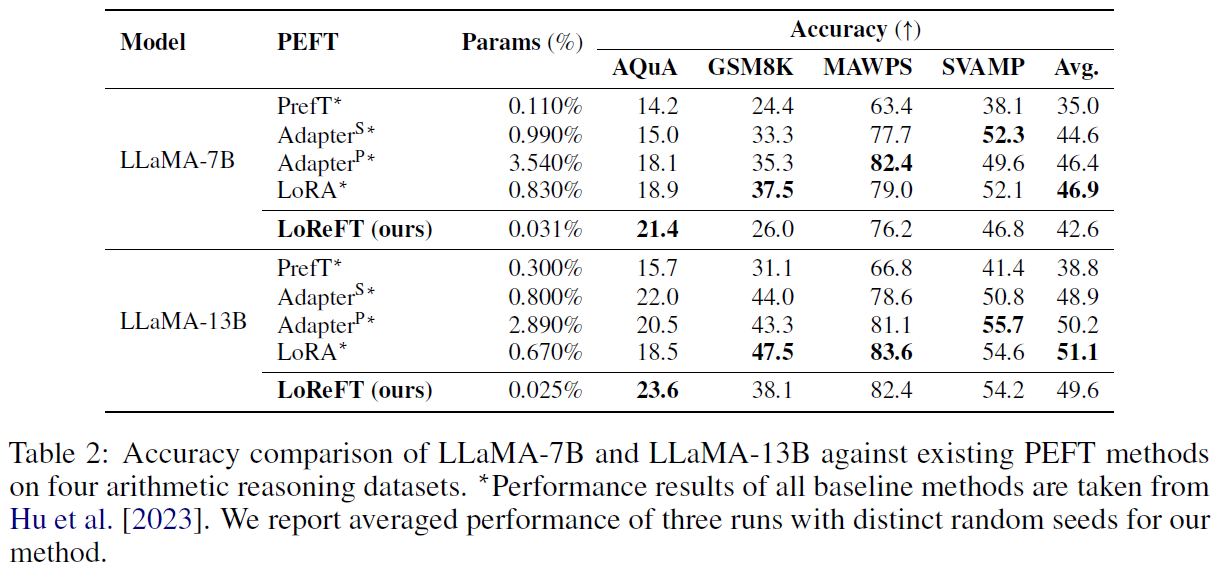
In the above table from the paper, we see again a much lower number of params for LoReFT. Here we see that results do not reach the performance of LoRA on 3 of the 4 evaluated datasets, yet keep in mind that much less weights are used comparing to the weights count used for LoRA here.
Instruction Following
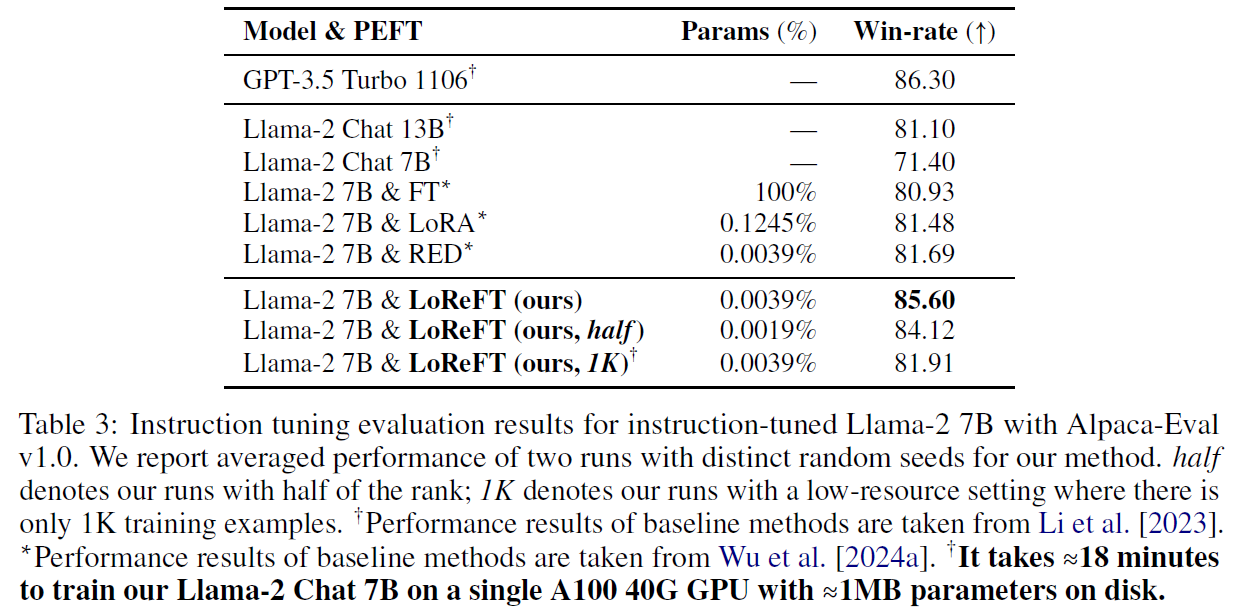
In the above table from the paper, GPT-4 is used as a judge to decide between the listed model in the table to text-davicin-003. Impressively, one of the LoReFT versions achieves the best win-rate from the evaluated open-source models.
Links & References
- Paper page – https://arxiv.org/abs/2404.03592
- Code – https://github.com/stanfordnlp/pyreft
- Join our newsletter to receive concise 1 minute read summaries of the papers we review – https://aipapersacademy.com/newsletter/
All credit for the research goes to the researchers who wrote the paper we covered in this post.