
Introduction
In the recent years, we witness remarkable success driven by large language models (LLMs). While LLMs perform well in various domains, such as natural language problems and code generation, there is still a lot of room for improvement with complex multi-step and algorithmic reasoning. To do research about algorithmic reasoning capabilities without pouring significant amount of money, a common approach is to focus on simple arithmetic problems, like addition, since addition of large numbers is a multi-step calculation. In this post we cover a fascinating recent research paper titled: Transformers Can Do Arithmetic with the Right Embeddings, which presents a remarkable progress in the arithmetic capabilities for transformers, which are the LLMs backbone.
Before diving in, if you prefer a video format then check out the following video:
Positional Embeddings
Say that we have a transformer we want to use, and we have a sequence of tokens which want to feed into the transformer. We do not just feed the sequence of tokens to the transformer but rather we usually add positional embeddings to the tokens sequence, to hint the transformer about the position of each token in the input sequence.
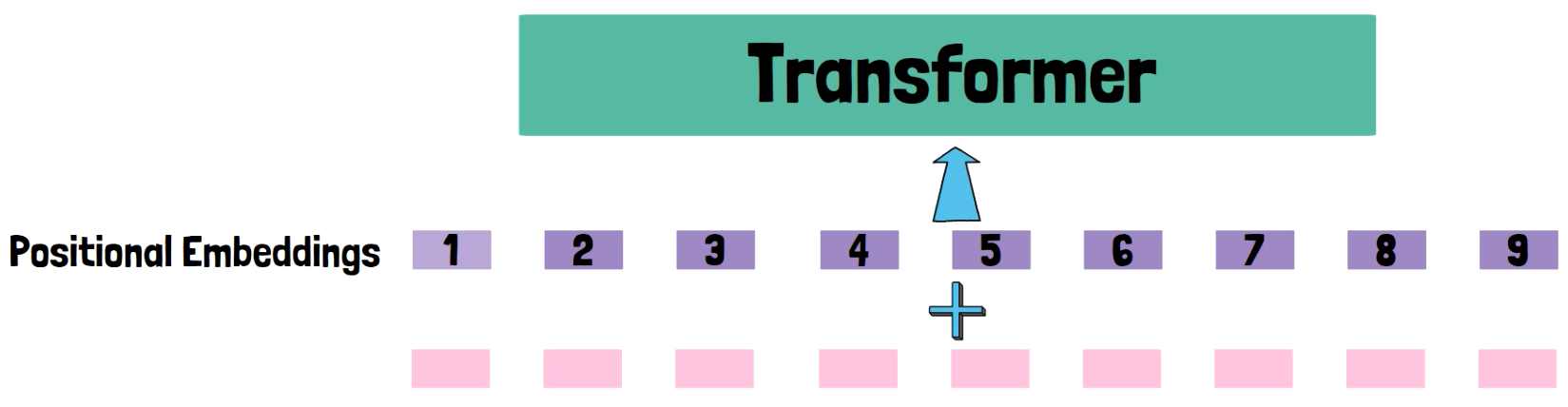
Human-like Addition
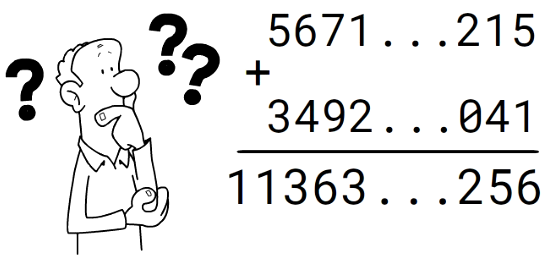
When humans calculate addition of large numbers, we organize the digits in columns by the digit position in each number, and positional embeddings until now do not embed the position of each digit in each number, but rather just the position of the token in the whole sequence.
Abacus Embeddings
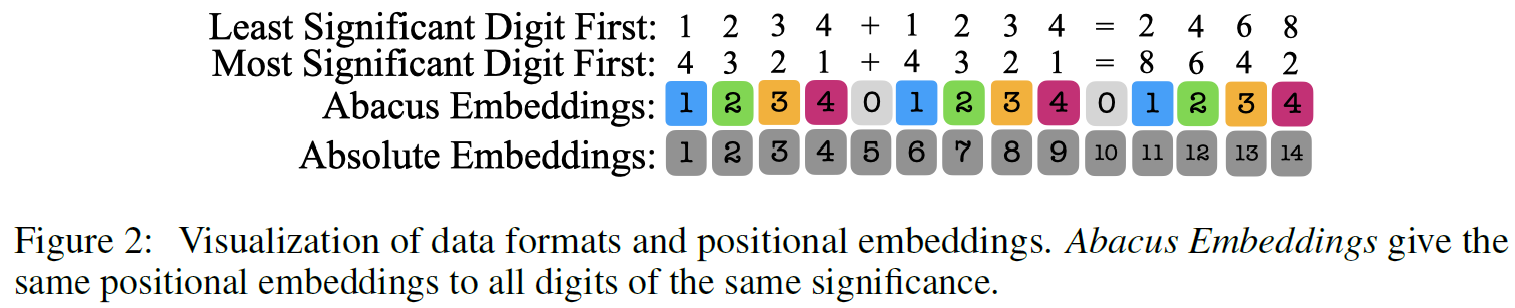
The progress made in this paper is achieved using a new type of positional embeddings, called Abacus Embeddings, which we can learn about using the above figure from the paper. We see at the top an addition of two numbers and the result, one time when writing the numbers with the least significant digit first and the other with the most significant digit first. In previous research it was shown that starting with the least significant digit can improve the results, and this paper adopts this as well. Then, on the bottom we see absolute embeddings, which as we said, provide hint about each token location in the sequence, but not about the location of each digit inside each number. We can see it is just an ascending sequence here. Abacus embeddings on the other end, provide the same value for all digits in the sequence of the same significance. So, the first digit of each of the numbers is assigned with the value 1, the second digit of each number is assigned with the value 2, and so it goes. We see that the first digit is assigned with the number 1, but in training we can start with a large number as well, to be ready for numbers with larger number of digits in test time.
Results
Let’s now take a look on how transformers perform when using Abacus embeddings.
Abacus Embeddings Logical Extrapolation
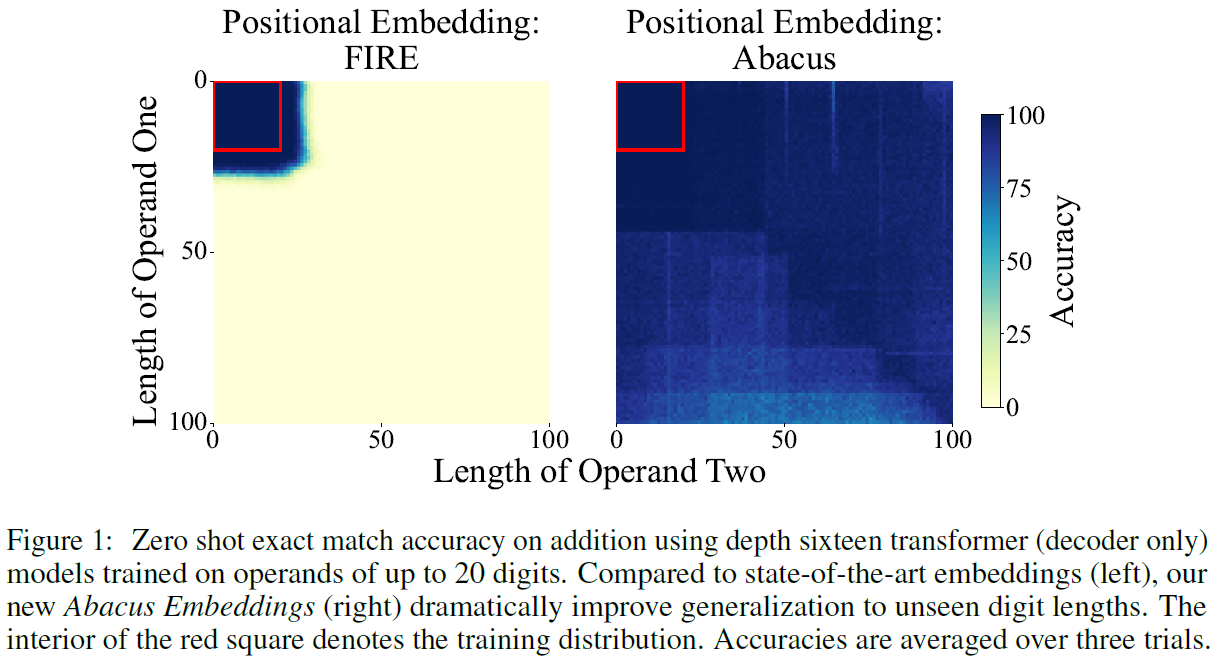
What we ask with logical extrapolation is whether the model can solve problems of greater size and difficulty than those that appear in the model’s training set. In the above figure from the paper, we can see results for two transformers that were trained from scratch. One with the new Abacus embeddings, on the right, and one with FIRE embeddings, on the left, which are the state-of-the-art embeddings for this task prior to this paper. The results are accuracy for adding two numbers, where the number of digits that each operand has is represented by the x and y axes, and the accuracy is reported with the color for each combination of digits count, where dark color means high accuracy and bright color means low accuracy. The red square of size 20 X 20 shows the digits count which the models were trained on. And we can see that there is a dramatic improvement for unseen numbers length when using the Abacus embeddings, achieving almost perfect accuracy for numbers up to 100 digits while being trained on numbers up to 20 digits.
Abacus Embeddings with Input Injection
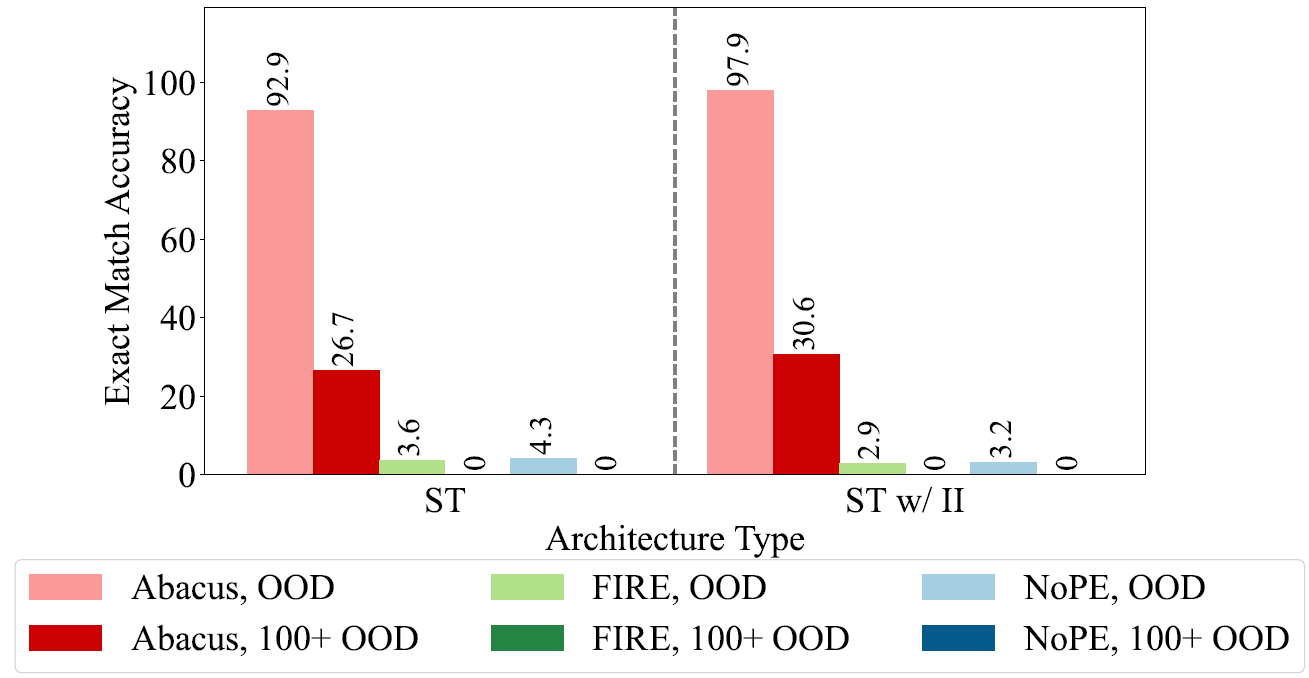
By input injection the meaning is that the input sequence is injected, using skip-connections, to any layer of the transformer. On the left, we can see results for a standard transformer, where the transformer with Abacus embeddings is in pink and red. Both reported results are out of distribution (OOD), meaning for larger numbers than the ones in training, and the darker red are numbers with more than 100 digits. On the right, we see the results when also adding input injection, which improves the results nicely for Abacus embeddings, from 92.9 to 97.9.
Recurrency Improves Arithmetic Reasoning
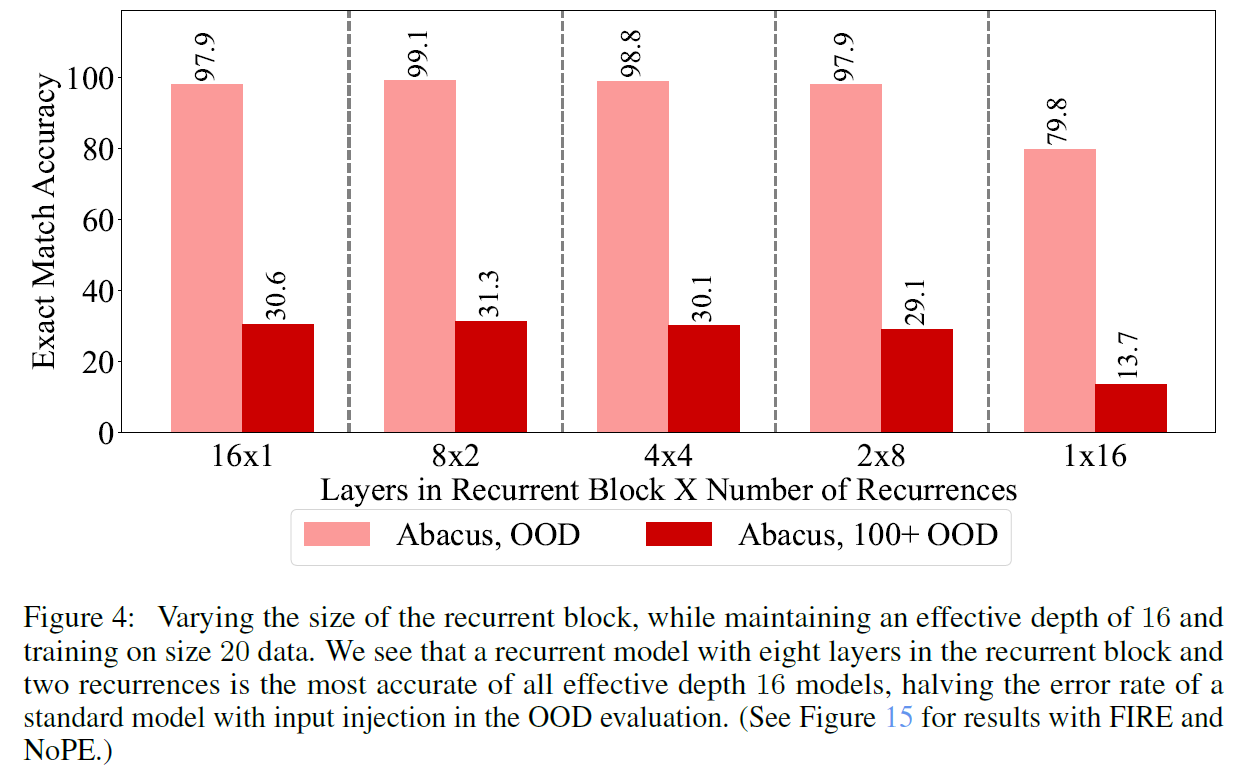
The best result is achieved when also adding recurrency. Meaning that each layer is used more than once in a forward pass of the transformer. In the above figure from the paper, we can see that the best result, with 99.1 accuracy is achieved when using a transformer with 8 layers where each layer is used twice in a single pass.
References & Links
- Paper page – https://arxiv.org/abs/2405.17399
- Code – https://github.com/mcleish7/arithmetic
- Join our newsletter to receive concise 1 minute read summaries of the papers we review – https://aipapersacademy.com/newsletter/
All credit for the research goes to the researchers who wrote the paper we covered in this post.