rStar-Math by Microsoft: Can SLMs Beat OpenAI o1 in Math?

Introduction

Large language models (LLMs) have become incredibly powerful, also demonstrating skills in the field of mathematics to some extent. The standard approach involves using a single model inference, where we feed the LLM with a problem, hoping to get a correct answer in response. This method is known as System 1 thinking.

System 1 vs System 2 Thinking

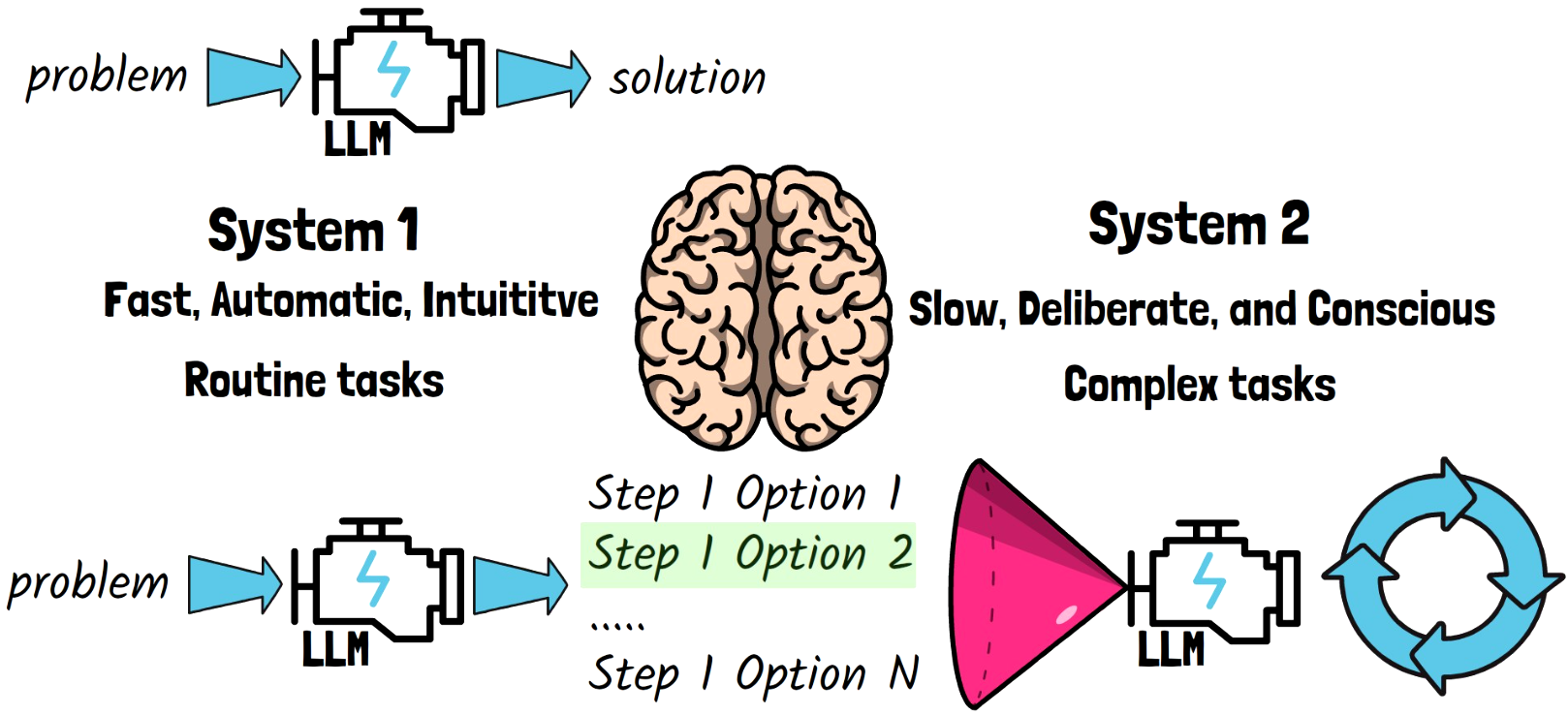
The concept of System 1 thinking comes from Daniel Kahneman’s book, Thinking, Fast and Slow. It describes two modes of cognitive processing: System 1 and System 2. System 1 is is a fast, automatic, and intuitive mode of thinking that operates with little to no effort. It’s used for routine tasks and decisions.. On the other hand, System 2 thinking is a slow, deliberate, and conscious mode of thinking that requires intentional effort. It is used when the information presented is new, complex, or requires conscious thought.

Applying System 2 thinking concept to solving math problems with AI, rather than providing a complete solution in a single run, the model yields multiple options for the next step in the solution. Another model then inspects the proposed options and chooses which step to take. This iterative process continues, with the model on the left yielding options for the next step and the model on the right choosing how to proceed, until the final solution is achieved.

Introducing rStar-Math

Not long ago, we witnessed a dramatic breakthrough in AI with OpenAI’s release of the o1 model which demonstrated remarkable skills in solving math problems. In this post, we dive into a recent paper by Microsoft, titled rStar-Math: Small LLMs Can Master Math Reasoning with Self-Evolved Deep Thinking. This paper demonstrates that Small Language Models (SLMs) can rival the math reasoning capability of the o1 model, by exercising System 2 deep thinking through Monte Carlo Tree Search (MCTS).

Monte Carlo Tree Search Deep Thinking in rStar-Math

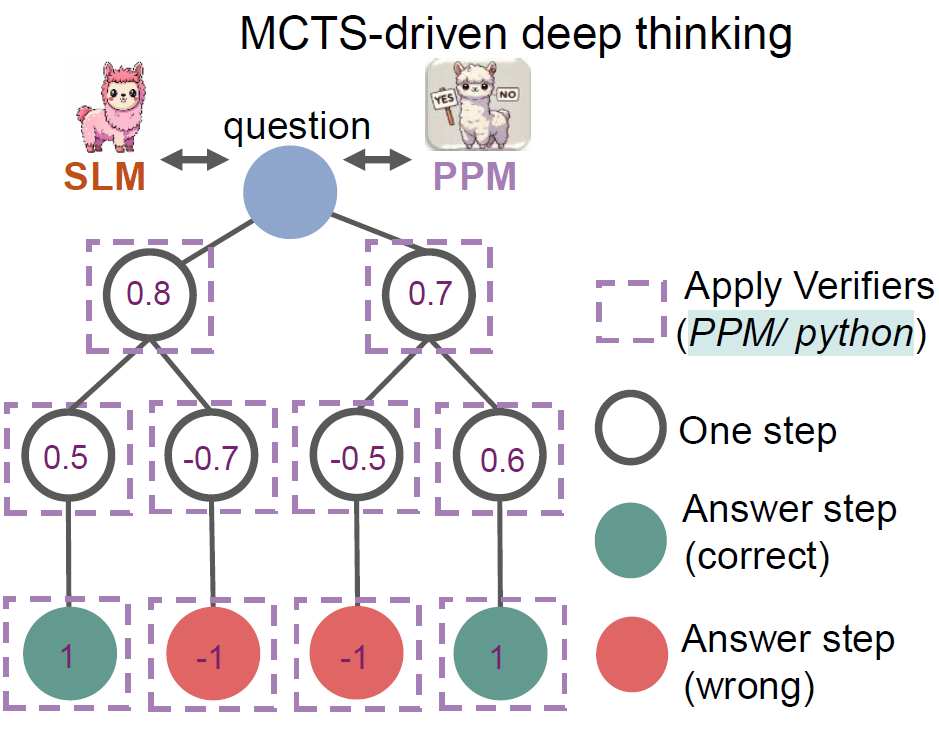
Let’s understand what Monte Carlo Tree Search deep thinking involves, using the following figure from the paper.

Policy Model and Process Preference Model

We have two Small Language Models (SLMs):

• The policy model generates reasoning step options.
• The process preference model (PPM) takes action by choosing the best reasoning steps.

Monte Carlo Tree Search (MCTS) Tree Structure

At the root of the tree, we have a math question to solve. The policy model generates options for the reasoning steps. First, it generates options for the first reasoning step. Then from each option, it generates options for the second reasoning step. The leaves are final answers, where green ones represent correct answers and red ones represent wrong answers. The path from the root question to the leaf nodes is called a trajectory.

The values we see on the nodes are Q-values. The Q-values represent the quality of the step based on its contribution to reaching a final correct answer. For the answer steps, correct answers are assigned a value of 1, and wrong answers are assigned a value of -1.

The process preference model (PPM) predicts a Q-value for each step. Using rollouts, it refines the Q-value. Rollouts simulate the outcome of proceeding with a certain step, helping to determine the final Q-value. Whether we end with a correct answer or not. We can conduct multiple rollouts and see how many times we reach a correct answer versus a wrong answer to determine the final Q-value of that step.

Achieving Accurate Reasoning Steps in rStar-Math

A key observation is that to develop capable policy and process preference models, we need to train the models with accurate reasoning steps and not just final answers, and it is extremely challenging to create such a dataset at scale, especially for complex math problems.

Perhaps we could use a strong existing LLM such as GPT-4 to extract accurate reasoning steps? Unfortunately, when tackling complex math questions, even top LLMs struggle to solve them correctly.

There are two methods by which rStar-Math achieves accurate reasoning steps:

1. Correct Answer-Based Reasoning Steps: Only include reasoning steps that led to a correct answer in the MCTS by comparing the predicted answers with ground truth labels. However, reaching a correct final answer does not guarantee that all reasoning steps were accurate. The next method helps with that.
2. Code-Augmented Chain-of-Thought: This novel method generates reasoning steps in natural language along with corresponding Python code for each step. Only samples where the Python code executed successfully for all steps are kept.

Code-augmented Chain-of-Thought (CoT)

Let’s understand Code-augmented CoT using the above example from the paper:

• At the top, we have a math question asking how far a person is from a certain point.
• Below, on the left, we see a code-augmented CoT reasoning for that problem. In a code comment, we have the natural language part of each step, followed by Python code.
• Only samples where the Python code executed successfully for all steps are kept.

The reasoning steps generated with MCTS are created using this Code-augmented CoT, which helps to ensure that the intermediate steps are correct in addition to the final answer.

The rStar-Math Framework

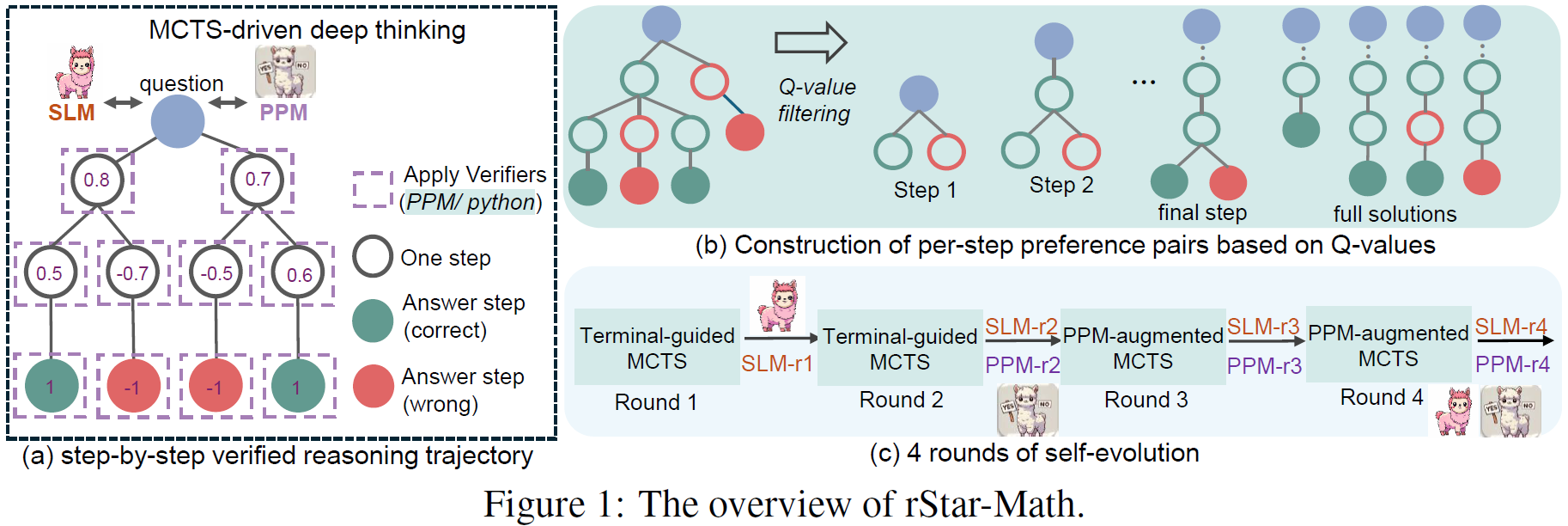
We can learn about the overall rStar-Math framework using the above figure from the paper. On the left, we see the Monte Carlo Tree Search deep thinking illustration which we reviewed earlier. In this section we focus on how we train the policy model and the process preference model.

Training The rStar-Math Models

Both models start from a pretrained small language model.

• The policy model, which generates the reasoning steps, is trained using supervised fine-tuning on correct reasoning steps. As mentioned above, these steps are extracted using Monte Carlo Tree Search with code-augmented chain-of-thought.
• The process preference model is trained using reinforcement learning. Below we describe how how positive and negative samples are constructed.

rStar-Math Reinforcement Learning Training Data

Looking at section (b) in the rStar-Math framework figure above, we can understand how training data is gathered for the process preference model. Given a search tree, we have trajectories that lead to correct answers and incorrect answers. For each step, we construct pairs of positive and negative samples.

In the above example, taking the right direction in the first reasoning step will lead to incorrect answer and is therefore used as the negative sample, while the left direction represents the positive example.

We construct the positive and negative samples similarly for the second step. Note that the preceding path from the root is identical, and we just construct positive and negative single steps added to this identical path.

In practice, our trees are more complex, and the selection of positive and negative samples is based on the Q-values of the nodes, representing each step’s contribution to a correct answer. This also helps rank multiple steps leading to a correct answer by the frequency in which taking that step results in a correct answer.

For the final answer step, ideally, we would do something similar. However, it is not always possible to find samples that lead to a different answer from an identical path. In such cases, we take two trajectories for a correct answer and two wrong answer trajectories as positive and negative samples.

rStar-Math Self-Evolved Deep Thinking

To achieve high quality models, the researchers suggest a recipe for Self-Evolved Deep Thinking, illustrated at section (c) in the rStar-Math framework figure.

rStar-Math Training Dataset

The self-evolution process consists of 4 rounds, and utilizes a curated dataset of 747k math problems.

• The dataset only contains math problems with final answer ground-truth labels, without reasoning steps. The reasoning steps are generated as part of the self-evolution framework.
• An important note is that it only includes competition-level problems, as simpler problems do not significantly contribute to improving complex math reasoning.
• Approximately 10 thousand samples were collected from existing datasets, and the rest were synthesized using GPT-4.

rStar-Math Bootstrap Round

The first round in the self-evolution process is a bootstrap phase. The pretrained SLM is not yet capable of generating high-quality data with code-augmented CoT reasoning. Therefore, a pretrained LLM with 236 billion parameters, DeepSeek-Coder-V2-Instruct, is used to generate the reasoning steps using Monte Carlo Tree Search with code-augmented chain-of-thought.

Note that only a subset of the original dataset is actually used since many problems were not solved correctly by the model. The policy model, which is initialized from a SLM, is fine-tuned on the verified reasoning trajectories. The process preference model is also initialized from a SLM and trained in this phase using reinforcement learning. However, its quality in this phase is not good enough yet.

Terminal-Guided MCTS

Until the process preference model reach a sufficient quality, the Monte Carlo Tree Search is not guided by it. Instead, it is terminal-guided. This means that to calculate the Q-value of each step, more rollouts are needed to see how many times a certain node leads to a correct answer. Unlike when there is already a high-quality process preference model that helps to start with a valuable Q-value before conducting rollouts.

Subsequent Rounds

At the end of the first round, we have the first version of the policy model, called SLM-r1. This model now serves as the policy model in the second round, replacing the LLM that was used for bootstrapping. The process preference model is still not of high quality, and therefore, in this phase, we continue to conduct a terminal-guided MCTS.

Similarly to the first round, the policy models generates reasoning steps for samples from the dataset and continue training both the policy model and the process preference model.

In the third and fourth rounds, we use both the policy model and the process preference model that we trained up to that point to generate reasoning steps and keep training them using these generated steps.

rStar-Math Gradual Improvement

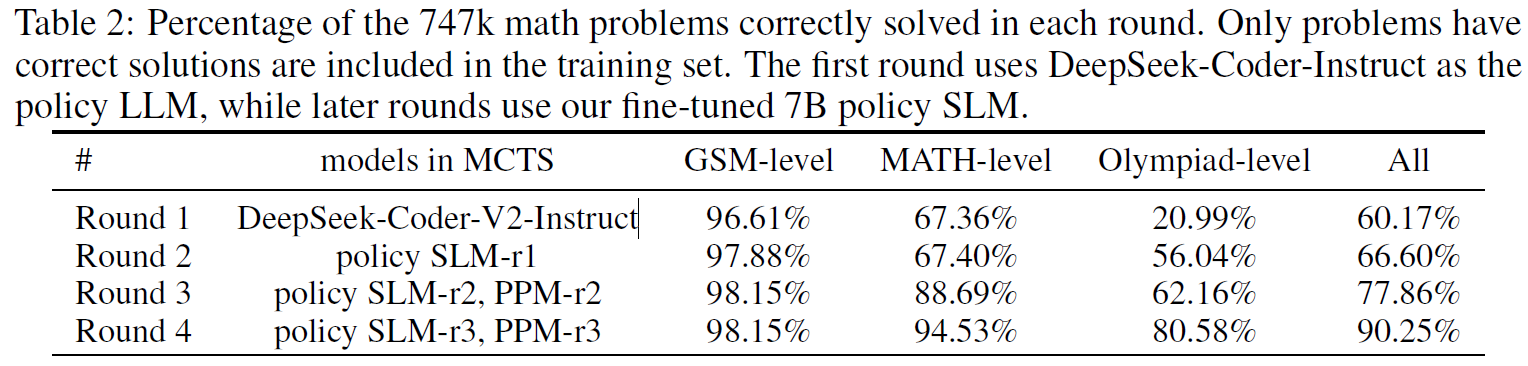
In the above table, we can see the percentage of problems that were solved correctly in each round, showing the improved capabilities as we proceed. This improvement is especially noticeable for the Olympiad-level problems.

rStar-Math State-of-the-art Level Mathematical Reasoning

To demonstrate the value of rStar-Math, we can see in the above table three versions of rStar-Math models, each starting from a different pretrained small language model. Impressively, the 7 billion version is comparable to, and in some cases surpasses, the o1-preview and o1-mini models.

References & Links

• Paper
• Code (not released yet when writing this line)
• Join our newsletter to receive concise 1-minute read summaries for the papers we review – Newsletter

All credit for the research goes to the researchers who wrote the paper we covered in this post.