In this post we break down DeepSeek’s “mHC: Manifold-Constrained Hyper-Connections”, which may be a crucial building block for how LLMs are built in 2026.

Introduction
About the same time last year (early January 2025), DeepSeek revolutionized the AI industry with the release of DeepSeek-R1. Now, DeepSeek set a great start for 2026 with a fascinating new paper titled “mHC: Manifold-Constrained Hyper-Connections”, which is already generating significant hype as a possible driver for the next major AI breakthrough in 2026.
This paper builds on an earlier paper from ByteDance called Hyper-Connections, but we don’t assume prior knowledge of this paper in this review. But before looking at hyper connections, we need to first talk about residual connections to properly understand the motivation of the paper.
Residual Connections
In the above figure from, we see an illustration of a standard residual connection, first introduced with ResNet, way back at 2016. This diagram doesn’t show a full model, but rather it shows a single residual block, which illustrates the idea of a single residual connection.
Residual Block Flow
At the bottom, we start with an input x_l which is coming from the previous layer of the model. From there, the signal is flowing in two paths.
- On the right, the input is processed by a module F. This module can be a feed forward network, a self-attention block, or any other architectural module we use.
- On the left, the residual stream simply passes the original input forward unchanged.
These two streams are then combined by an element-wise sum, forming the output of the block, defined by the following formula:
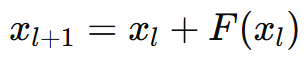
The Success of Residual Connections
The residual connections paradigm has established itself as a fundamental design element in the large language models (LLMs) we use today.
While the above figure shows a single layer, when stacked across many layers, residual connections allow the original input signal to propagate deep into the network which helps to preserve information.
Residual connections succeeded thanks to their contribution for training stabilization of deep networks and enablement of large-scale training. One main reason for that is that they help mitigate vanishing gradients.
The propagation of the input without modifications adds an identity mapping to the function we optimize in training, which has a constant gradient of 1, mitigating cases where the gradient of the F module becomes very small.
Residual Connections Are A Decade Old
Interestingly, over the last decade, we’ve seen enormous innovation with what happens inside the module F, with new attention mechanisms, mixture of experts, and many more. But the residual connection itself has remained almost completely unchanged since 2016.
That’s exactly the gap that Hyper-Connections aim to address.
Hyper-Connections
Hyper-Connections were introduced in a paper from ByteDance in 2025 with the goal of generalizing residual connections. We can understand the idea using the above figure, which shows a Hyper-Connections (HC) block next to a standard residual block.
At a high level, Hyper-Connections (HC) extend the residual connection concept by widening the residual stream itself. Instead of a single residual vector, the residual is now expanded into multiple components that are mixed together at every layer using learned mappings.
Hyper-Connections (HC) Flow
At the bottom of the HC diagram, we see that the input is now expanded multiple times, four in this example. These form the residual stream maintained by the model. Initially, they are identical duplicates of the same input.
On the left of the HC diagram, we see the wider residual stream. Now that we have multiple inputs flowing in that stream, they are mixed together using a learnable residual mapping matrix. Instead of having a fixed identity path at each layer, Hyper-Connections allow the model to learn how information is mixed and propagated across the residual stream.
Importantly, this added flexibility doesn’t significantly increase computation. This is because the expansion rate is typically small, such as 4 as we see here.
On the right side of the block, the expanded input is first projected back down to the model dimension before being processed by the module F. This means we don’t pay the computational cost of the expanded representation inside expensive components like attention or feed-forward layers.
The output of module F is then expanded using another learnable matrix, and afterwards it is combined with the residuals, forming the output of the block and the input for the next layer.
Hyper-Connections Expressivity vs Stability
There’s no doubt that this design gives the model more expressive power along the residual stream. The network has much more flexibility in how information flows across layers.
However, this flexibility comes with a cost. In standard residual connections, the identity mapping is guaranteed by the architecture itself. This guarantee is crucial for stabilizing high-scale deep networks training. A key observation by DeepSeek is that Hyper-Connections violate this promise.
Hyper-Connections rely on learned mixing weight matrices, which are unconstrained. As a result, the residual stream can drift away from the identity mapping, causing signal magnitudes to either explode or vanish during both the forward pass and backpropagation.
This phenomenon breaks the fundamental premise of residual learning, which relies on unimpeded signal flow, and leads to training instability in deeper or larger-scale models. This is exactly the problem that DeepSeek addresses with Manifold-Constrained Hyper-Connections (mHC).
Manifold-Constrained Hyper-Connections (mHC)
To address the instability introduced by Hyper-Connections, DeepSeek does not remove their flexibility. Instead, the core idea behind Manifold-Constrained Hyper-Connections is to preserve the full expressive power of Hyper-Connections while restoring the identity guarantee that made residual connections work in the first place.
If we look closely at the illustration, the mHC block is almost identical to the Hyper-Connections block. The structure is the same, and information flows in the same way. The crucial difference is with the residual mixing matrix, which is no longer unconstrained. Instead, it is now subject to additional structural constraints designed to stabilize signal propagation across layers.
mHC Residual Mixing Matric
Rather than allowing the residual mixing matrices to take arbitrary values, Manifold-Constrained Hyper-Connections enforces two constraints on the residual mixing matrix.
- All entries must be non-negative,
- Each row and column must sum to one.
Matrices with these properties are called doubly stochastic, and in practice these constraints are enforced using a classic algorithm from 1967 known as the Sinkhorn–Knopp algorithm.
Intuitively, this means two things. One, every output residual receives the same total amount of input signal. And second, every input residual contributes the same total amount to the outputs. As a result, the widened residual stream preserves an identity-like residual at a global level, even though information is still free to mix across multiple paths.
What Changes With The Other Matrices?
The pre and post projection matrices differ from those used in standard Hyper-Connections as well. Here, DeepSeek enforces non-negativity on these mappings using a sigmoid function.
The intuition behind that is that the composition of positive and negative coefficients in these projections can lead to signal cancellation, since signals may cancel each other out, which can then destabilize training at scale.
mHC Results
DeepSeek evaluates Manifold-Constrained Hyper-Connections using large language model pre-training across three variants:
- A baseline model without Hyper-Connections.
- A model with standard Hyper-Connections,
- A model with the proposed Manifold‑Constrained Hyper‑Connections (mHC).
All models use mixture-of-experts architectures inspired by DeepSeek‑V3, and both Hyper-Connections and Manifold‑Constrained Hyper‑Connections use an expansion rate of 4 for the widened residual stream size.
Benchmarks Comparison
We begin with the following table from the paper, which compares 27 billion parameter models for each of the variants across multiple downstream benchmarks. Both the Hyper-Connection models outperform the baseline, confirming that widening the residual stream can drive performance improvements.
More importantly, Manifold-Constrained Hyper-Connections consistently achieves the strongest results, as shown in the bottom row of the table. This indicates that Manifold-Constrained Hyper-Connections preserves the benefits of Hyper-Connections while delivering broadly improved downstream performance.
Training Stability of HC vs mHC
In the left plot, we see that the Hyper-Connections model begins to show instability around the 12,000th training iteration, with its loss diverging significantly from the baseline. In contrast, Manifold‑Constrained Hyper‑Connections relatively mitigates this issue as we can see in the bottom line.
The right plot shows gradient norms. Here, Hyper-Connections clearly shows instability, while Manifold‑Constrained Hyper‑Connections mitigates that completely by closely following the baseline, indicating smooth and well‑behaved gradients throughout training. This confirms that Manifold‑Constrained Hyper‑Connections successfully restore the training stability.
Resources
- mHC Paper
- HC Paper
- ResNet Paper
- Join our newsletter to receive concise 1-minute read summaries for the papers we review – Newsletter
All credit for the research goes to the researchers who wrote the paper we covered in this post.
